パラメーター確率分布を用いたプラントモデル自動更新技術
キーワード:制御特性変化把握,システム同定,確率分布,最適化,CO2削減,SORTiA™
アズビルでは制御・最適化によるCO2削減に取り組んでおり,制御高度化ソリューションSORTiA™もその一端を担っている。高度制御ではプラントの特性を表したモデルを用いるが,何らかの理由でプラントの特性が大きく変化した場合にモデルがそのままであると,その差異から制御・最適化の性能が低下し得る。この課題を解決するため,操業中のプラントのモデルを自動で推定して更新する技術を開発した。開発した技術は操業中のプラントデータからモデルのパラメータの確率分布を推定し,その分布に基づいてモデルの更新要否を自動で判断する。本技術はプラントへの特別な操作が不要で,モデルの維持が容易という特長がある。
1.はじめに
アズビルは脱炭素社会の実現に向けて,お客様現場におけるCO2削減に取り組んでいる。CO2削減の手段は多種多様だが,その一つとしてエネルギーの最適化がある。当社は現場で培った知見と制御技術を結集した制御高度化ソリューションSORTiAを提供している(1)。SORTiA の中核に位置する多変数モデル予測制御SORTiA-MPC(MPCはModel Predictive Controlの略称)は石油精製をはじめとする製造プラントや,様々な業界の動力装置に導入されており,制御・最適化による省エネルギーを通じたCO2削減に貢献している。
高度制御の導入はCO2削減やオペレーション負荷低減に大きな効果があるが,課題としてモデルの構築と維持がある。このモデルとは,制御・最適化の対象であるプラントの振る舞いを単純化して数式で表したものである。高度制御の性能はモデルによるところが大きく,価値を生み出すにはモデルがプラントの振る舞いの主要な部分を表現できる必要がある。そのような,制御・最適化に必要な精度を持ったモデルを導入時に構築し,導入後に維持することが,高度制御適用における重要なポイントの一つとなる。
この導入後の維持に関し,プラントは経年変化の蓄積や装置の修繕・改造などによってその特性が変わり得るという課題がある。プラントの特性が変わるとその分,モデルの誤差(プラントとの差異)が拡大する。誤差が小さければ,SORTiA-MPCなどの高度制御はフィードバック制御によってその影響を抑制できる。そのため,モデルの小さな誤差が大きな制御性能劣化に直結することは無い。しかし,プラントの特性の変化が大きく,モデルの誤差がさらに拡大すると,性能に影響する場合がある。このような場合は,プラント側の変化にモデルの方を追従させることが,高度制御の効果を維持するために望ましいと考えられる。これがプラントモデルの更新技術が求められる背景である。
アズビルでは操業中のプラントデータから自動でモデルを推定し,更新する技術の開発を行っている。操業データは量的には豊富だが,その中でモデル推定可能な状態にある部分は限られており,その限られたデータを選別する必要がある。しかし,このデータ選別を人手で行うのは専門家でも大変な労力である。そこで,我々はモデルを表す数式のパラメータの確率分布を推定することでデータを選別し,モデルを自動で推定・更新する手法を新たに開発した。本稿ではこの技術について説明する。
2.モデル自動更新実現の課題
本章ではプラントモデルとその自動更新について述べ,その実現における課題について説明する。
2.1 プラントのモデルと更新の必要性
ここで扱うプラントのモデルは,プラントに入力を与えた際の出力の振る舞い,すなわち入出力関係を数式で表した数式モデルである(図1)。高度制御で対象となるプラントは動特性を持つので,そのモデルも動特性を表現可能な伝達関数,状態空間表現,微分方程式などが用いられる。SORTiA-MPCでは伝達関数を用いている。
モデルは入力を与えられると,プラントの振る舞いについて数式を使って計算して模擬し,プラントとおおむね同じ出力を算出する。これを利用してプラントの出力を予測できる。また,望ましい出力を得るために必要な入力を逆算できる。これにより制御・最適化が可能になる。
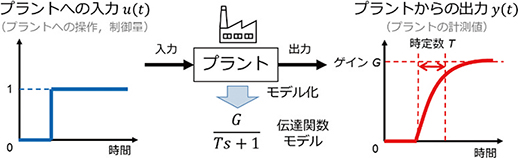
図1 プラントのモデル
モデルを利用した制御・最適化はプラントの特性が変化するとその影響を受ける。変化が小さい場合は,制御・最適化によってその影響がある程度吸収されるので,あまり問題にならない。一方,変化が大きくなると,モデルがプラントを必要な精度で模擬できなくなり,制御・最適化が本来の性能を発揮できなくなる。これを避けるには,プラントの特性が大きく変化したらモデルの方をプラントに合わせて更新し,両者の差異を性能に影響しないレベルまで小さくする必要がある。それにより高度制御の効果を維持することがモデル更新の目的となる。
2.2 操業中プラントデータによるモデル更新の狙い
モデル更新手法として,我々は通常操業中のプラントデータを用いる手法の実現を目指した。
実は,プラントモデルの推定はプラントの入力に試験用の摂動を加えると容易になる。そのため,高度制御導入時のモデル構築では試験用入力をプラントに与え,通常とは異なる操業状態にして行うことが一般的である。しかし,この方法は試験用の摂動を加えた時しか推定できない上,試験用の摂動が操業に与える影響に配慮する必要があり,モデル更新にそのまま適用することは適切でないと考えた。そこで本開発では,通常とは異なる特別な操業が不要なモデル更新手法を目指すことにした。
通常操業中の制御データは入手が容易なので,そのデータからプラントのモデルを推定できれば,広範な対象や状況に適用でき使いやすい手法になると考えた。
2.3 操業中プラントデータによるモデル推定の課題
本節では,通常操業中のプラントデータによるモデル推定の難しさと解決すべき技術課題について説明する。
プラントデータからプラントの数式モデルを推定することは,プラントの入出力関係を表す数式を推定することである。そのためには,入出力データが以下の条件を満たす必要がある。
- A) 入力に十分な変動があること
- B) 出力には入力の変動に応じた変化が明確に現れており,外乱の影響が小さいこと
入出力関係を表す関数をデータから求めるには,入力は一定ではなく変動が必要である。また,外乱の影響で入出力関係が不明瞭になったデータからはモデルを必要な精度で推定できない。
上記条件は通常操業中にモデル推定する難しさを示唆している。高度制御が適切に運用されたプラントは入出力ともに変動が小さく安定していることが多く,条件A)を満たさない。また,プラントは様々な要因の外乱を受けるが,その影響が大きい場合は条件B)を満たさない。試験用の摂動を与える方法では入力の能動的操作が可能だが,目指す手法は操業中データが上記条件を満たす状況を受動的に待つ必要がある。ここが,通常操業中にモデルを推定する難しさになる。
一方,実際の操業中データを観察すると,上下限設定の変更などで入力が変化し,かつ外乱の影響が小さい区間があることに気付く。このような貴重な機会を捉えてプラントのモデルを推定すれば,目指すモデル自動更新が可能になると考えた。つまり,操業中データから前述の条件を満たす区間を自動で選別し,モデル推定に不向きな区間を除くことが,解決すべき課題となる。
3.提案手法の考え方と手順の概要
本章では提案手法(2)の考え方と手順の概要について説明する。提案手法で鍵となるのが推定に適した区間の自動選別だが,これを実現するため,提案手法ではモデルのパラメータの確率分布を推定して利用する。
パラメータの確率分布とはパラメータがある値を取る確率を関数として表したものである(図2)。パラメータの確率分布はこれまでも信頼区間という形で推定値の信頼性評価に利用されてきた。提案手法ではこれを区間の選別に利用する。もし,ある区間で推定したパラメータの確率分布が狭い範囲に分布していれば,その区間で推定したパラメータは不確かさが小さく信頼性が高いと考えられるので,モデル推定に適した区間と判定する(図2実線)。逆に分布が広ければ,モデル推定に適さない区間と判定する(図2破線)。このように,パラメータの確率分布を利用してモデル推定に適した区間を選別し,モデル更新することが,提案手法の最大の特長である。
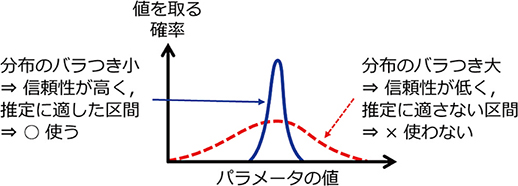
図2 パラメータの確率分布とモデル推定に適した区間
まず,3.1節で提案手法の問題設定について述べ,次に3.2節で提案手法の手順を説明する。
3.1 問題設定
プラントのモデルは既存のものがあり,モデルのパラメータは初期値が得られると仮定する。1章で述べた通り高度制御導入時には通常,プラントのモデルを構築するので,それを利用する。また,プラントの変化はモデルのパラメータの変化で表現可能と仮定する。これは,モデルの次数や構造は変わらないという仮定である。この仮定はプラントの変化の要因が経年変化の蓄積や装置の修繕,操業条件の変更であれば妥当だと考えられる。一方,プラントの構造が変わるような大きな改造の場合にはあてはまらないと考えられる。
以上の仮定のもと,プラントから定期的に入出力データを収集し,提案手法を実行する。
3.2 提案手法の手順の概要
提案手法は入出力データを区間に区切り,各区間でモデルのパラメータの確率分布を推定し,以下の3条件を満たした場合にモデルを更新する。
- A) パラメータの確率分布が狭く,推定に用いた区間がモデル推定に適していること
- B) 新たに推定したモデルから得られる出力の推定値が,現在使用しているモデルによる推定値よりもプラントの出力値に精度よく追従していること
- C) 新たに推定したモデルのパラメータが,これまで得られた確率分布から大きく外れていないこと
以下,提案手法の手順を順番に示す(図3)。収集した入出力の時系列データは,最初に同じ長さを持つ区間に分割する(図3では3つの区間に分割)。
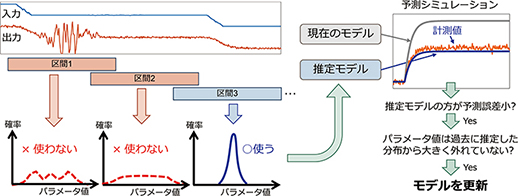
図3 提案手法の手順概要
- 分割された区間のデータを用い,プラントモデルのパラメータの確率分布を区間ごとに推定する(確率分布の推定方法は4章を参照)。
- 確率分布の分散を区間ごとに算出し,しきい値以下であればその区間は条件のA)を満たしたと判定して次の手順に進む。しきい値より大きい区間は使わない。
- 区間1は外乱の影響で確率分布の分散が大きいので使わない
- 区間2は入力の変動が小さいので使わない
- 区間3は入出力間の因果関係が分かるような明確な変動があり,外乱の影響も小さく,分散が小さいので,推定に用いる
- パラメータの確率分布の重みつき平均値を推定値としたモデルを生成する(ここでは区間3で推定した確率分布からモデルを生成)。
- 現在制御に使っているモデルと,手順3で生成した推定モデルの両方にプラントの入力データを与えてそれぞれシミュレーションを行い,出力予測値の時系列を得る。そして,対応する実際のプラントの出力計測値との誤差を算出する。
- 手順4で算出した誤差を両モデルで比較し,推定モデルの方における誤差が小さければ条件B)を満たしたと判定して次の手順に進む。
- 図3では推定モデルの方が計測値によく追従しており,誤差が小さいので,条件B)を満たしたと判定される。
- モデルの推定値を過去に推定した確率分布と比較し,大きく外れていなければ条件C)を満たしたと判定する。そして,条件A)~C)を全て満たしたらモデルを更新する。
4.モデルパラメータの確率分布推定手法
提案手法を実現するためには,動的モデルのパラメータの確率分布を推定する必要がある。本章では,このパラメータの確率分布を推定する方法について説明する。本章の記述は3章の手順1の詳細となる。
提案手法では,モデルのパラメータの確率分布を推定する手法としてベイズ推定を採用する。一般に,動的モデルのパラメータの確率分布を解析的に推定することは以下の理由から困難である。
- (1)ある時点の情報がそれまでの過去の情報に影響されるため,直接計算することが難しい。
- (2)全体の振る舞いを捉えるためにはすべての時点の情報を考慮する必要があり,この計算が複雑になることが多い。
このことから,パラメータの確率分布を直接計算することは困難であるため,提案手法における確率分布推定ではマルコフ連鎖モンテカルロ法(Markov Chain Monte Carlo:MCMC)という手法を用いる。MCMCとは,乱数を用いて多数の標本を生成し統計的な解析を行うことで,対象の分布を近似的に求める方法である。
本章の構成は以下の通りである。4.1節では離散時間の状態空間表現について,4.2節ではモデルのパラメータの確率分布を推定する手順について述べる。4.3節ではこの確率分布推定手法の背景について説明する。
4.1 モデル構造の離散時間状態空間表現
SORTiAでは,モデルを連続時間の伝達関数で表現している。一方,この確率分布推定手法では,離散時間の状態空間表現に基づくパラメータ推定手法を用いる。そのため,連続時間の伝達関数を離散時間の状態空間表現に変換する必要がある。本節では,この変換方法について述べる。
本報告書では,一入力一出力系を対象として説明する。例として,以下のようにむだ時間を含む1次遅れ系の伝達関数で表される系を考える。ただし,\(G\)はゲイン,\(T\)は時定数,\(t_d\)はむだ時間,\(U(s)\)と\(Y(s)\)はそれぞれ入力\(u(t)\),出力\(y(t)\)をラプラス変換したものである。
上式を逆ラプラス変換し,サンプリング周期\(Δ_t\)で後退差分近似を施すと,以下の離散時間の状態空間表現が得られる。ただし,システムノイズ\(v(t)\)と観測ノイズ\(w(t)\)を考慮する。
ここで,\(v(t)\)と\(w(t)\)は平均が0,分散がそれぞれ\(α^2\),\(β^2\)の正規分布に従う乱数であると仮定する。推定するパラメータはゲイン\(G\)と時定数\(T\),そして\(α\),\(β\)である。以下では,これらのパラメータをまとめて\(θ\)と呼ぶ。また,\(x\)を内部状態と呼ぶ。
本報告書では,一入力一出力系に限定して説明したが,多変数系についても同様に変換することが可能である。
4.2 パラメータ確率分布推定手順
提案するモデルのパラメータの確率分布推定手法では,離散時間の状態空間表現に基づくパラメータ推定方法として,SMC²という手法と同様のアプローチを用いる。SMC²とは,状態空間表現の対象に対して,パーティクルフィルタ(Particle Filter: PF)を用いてパラメータ\(θ\)と内部状態\(x\)を同時に遂次推定する手法である(3)。PFとは,粒子 (particle) と呼ばれる標本を用いて確率分布を推定する手法であり,遂次モンテカルロ法(Sequential Monte Carlo: SMC)の一種である。ここで,粒子一つひとつの位置は,推定対象である確率分布の確率変数に対応している。この粒子は重みを持っており,粒子を多数用いることで,その位置と重みによって確率分布を近似することが可能となる。PFは,それらの粒子の位置と重みを観測値に基づいて遂次的に更新することで,求める確率分布を推定するアルゴリズムである(4)。
本手法では,内部状態xの推定にカルマンフィルタ(Kalman Filter: KF)(5)を用いる。SMC²や本手法の内部で用いられるMCMCについては次節で説明する。
以下,本手法の手順を順番に示す(図4)。例として,図4では,パラメータ\(θ\)の事前分布として一様分布を設定する。なお,以下の手順は分割された入出力の時系列データの一つの区間に対して適用される。
- 事前知識をもとに,パラメータ\(θ\)の事前分布を設定する。
- 例えば,現在制御に使っているパラメータの値を中心とした一様分布を設定する。
- 事前分布に基づいて,初期の粒子の集合を乱数で生成する。それぞれの粒子に初期の重みを割り当てる。
- 以下の手順をある時刻の入出力値一組につき一回ずつ,反復処理として繰り返す。
- 粒子の位置や重みが一部に偏っている場合は,リサンプリングを行う。
- 乱数を用いて粒子の位置を更新する。
- 更新量はチューニングパラメータで決まる。
- KFを用いて,各粒子の内部状態\(x\)を推定する。
- 粒子の位置と状態空間表現におけるパラメータ\(θ\)の値が一対一で対応する。
- 対応するパラメータ\(θ\)の値を用いて,その条件下での内部状態\(x\)を推定する。
- 粒子の位置の遷移確率を計算し,更新後の粒子の位置を決定する。
- 各粒子の内部状態\(x\)を用いて,それぞれの位置の遷移確率を計算する。遷移確率とは,粒子がある状態から別の状態に変化する確率である。
- 確率が高い粒子は新しい位置に移動し,それ以外の粒子は元の位置に留まる。
- 観測された出力をもとに,粒子の重みを更新する。
- 推定した内部状態\(x\)から出力\(y\)を予測し,その予測値と実際の観測値の誤差を計算する。
- 誤差が小さい粒子は重みが増え,誤差が大きい粒子は重みが減る。
- 重みつき粒子を用いて,手順5のチューニングパラメータを更新する。
- 粒子の位置と重みが集まっている場合は,更新量が少なくなるように調整する。
上記の手順を区間の最終時刻まで行うことで,粒子の位置と重みがパラメータの確率分布に漸近する。その結果,モデルのパラメータの確率分布が推定できる。
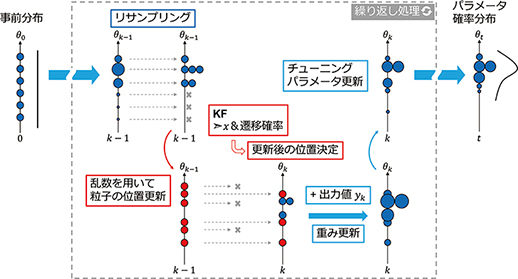
図4 パラメータの確率分布推定の概念図
図5に,モデル推定に適した区間において,推定するパラメータ\(θ\)の一つであるゲインの重みつき粒子が遷移する様子を,ヒートマップで表した図を示す。縦軸はゲインの推定値を,横軸は区間内の時刻である。時刻が進むにつれ,粒子が広がった分布から徐々に粒子が集まり,信頼性の高い確率分布に収束する様子が確認できる。
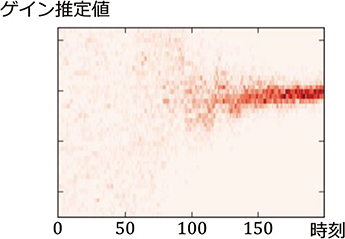
図5 重みつき粒子のヒートマップ
4.3 提案する確率分布推定手法の背景
本節では,前節で説明したパラメータ確率分布推定手法の各手順で使用されているアルゴリズムについて説明する。
まず,本手法が参考にしたアルゴリズムであるSMC²について説明する。この手法は手順6において,内部状態\(x\)の推定にKFではなくPFを用いる。PFを用いることで,より多くの対象に対してパラメータを推定できる。しかし,SMC²は二重にPFを構成するため,計算量がかなり多く,推定に多くの時間を要する。
そのため,本手法では,内部状態\(x\)の推定をKFに置き換えることで計算時間の短縮を図っている。一般的には,PFをKFにそのまま置き換えることは難しいが,今回はパラメータ\(θ\)がある値に固定されているため,4.1節の離散時間状態空間表現に対してKFを適用できる。
つぎに,各手順で使用されているMCMCのアルゴリズムについて説明する。
手順5では,ランダムに粒子の位置を更新しているが,ここではMCMCの遷移カーネルmを用いて粒子の位置を更新している。本手法では,遷移カーネルmの設計手法として,MCMCの一種であるメトロポリス・ヘイスティング(Metropolis-Hastings: MH)法(3)と呼ばれる手法を用いている。
手順7で計算される遷移確率とはMH法で用いられるMH比である(3)。このMH比を用いて遷移した新しい標本を受け入れるか,却下して現在の標本を維持するかを決定する。この操作によって,求める分布により近い分布に従う標本を得る。
手順9では,重みつき粒子の分布に基づいて,提案カーネル\(\tilde{ m }\)の チューニングパラメータであるガウス分布の共分散行列\(\Sigma\)と遷移回数を更新する。重みつき粒子の分布が狭くなると,粒子の遷移距離が小さくなり,遷移が繰り返されることで,重みつき粒子が集まり信頼性の高い確率分布に収束する。
5.数値シミュレーション
本章では,モデル予測制御で制御・最適化されているプラントのモデル更新を想定したシミュレーションにより,提案手法が通常操業中のプラントデータから動的モデルを推定できることを示す。
5.1 シミュレーション設定
対象の動的モデルは一入力一出力系として,1次遅れ系とする。対象であるプラントの変化により,プラントとモデルの間でゲイン\(G\)が異なっている状況を想定する。具体的なパラメータ値は表1のように設定した。
表1 パラメータの値

このプラントに対してSORTiA-MPCによる制御・最適化を行い,目標値が変化して入力(操作変数)が操作される状況をシミュレーションする。最適化の目的は入力値の最小化とする。最初,最適化により出力(制御変数)は上限値付近にあるが,途中で出力の上限値を表2のように変更する。それにともなって入力が操作され,変化することで,モデルが推定可能になることを期待している。
このシミュレーションにより得られた入出力データを図6に示す。横軸が経過時間,縦軸が入出力の変数値である。出力値と入力値をそれぞれ実線で,出力の上限値を破線で示した。出力には平均0,分散0.09の白色性外乱を常時印加している。それに加え,大きな外乱の影響で推定に適さない区間を模擬するため,2:30~5:00の区間では平均0,分散1.0の白色性外乱を追加している。なお,制御周期は1分である。
表2 出力の上限値設定

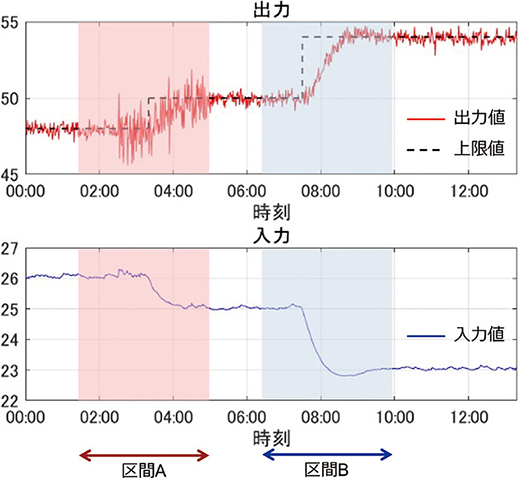
図6 シミュレーションの入出力データ
対象はモデル予測制御で制御されているが,プラントの実際のゲインより小さいゲインを持つモデルで予測,制御したため,操作入力が適切な量よりも過大になる。このため,出力値に9:00付近でオーバーシュートが発生し,出力値が上限値を一時的に違反している。ただし,SORTiA-MPCはモデル誤差に対してロバスト性があり,その影響を制御によって抑制できるので,違反は小さい量に留まっている。
なお,提案手法の設定は分割する区間の幅を200分,推定対象はゲイン\(G\)と時定数\(T\)とする。推定に用いるデータのサンプリング周期は制御周期と同じ1分である。
5.2 シミュレーション結果
推定結果を表3に示す。推定は,01:40~05:00の区間(以下,区間A)と06:34~09:54の区間(以下,区間B)の2つの区間で行われた(図6参照)。どちらも出力上限値の変更にともなう入力操作が含まれる区間である。また,区間Aと区間Bで得られた推定ゲインと推定時定数の確率分布をそれぞれ図7,図8に示す。
表3 推定結果

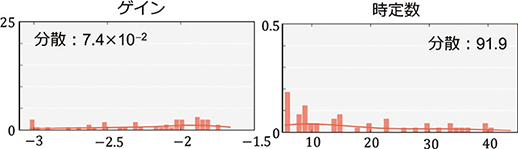
図7 区間Aで推定したパラメータの確率分布
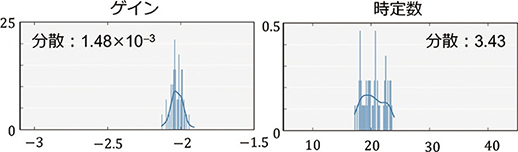
図8 区間Bで推定したパラメータの確率分布
区間Aでは,出力に大きな外乱が含まれており,入力操作による出力変化が不明瞭になっているため,パラメータの確率分布の分散が大きくなっている。一方,区間Bでは,外乱の影響が小さく,入出力間の因果関係が明確であるため,確率分布の分散が小さくなっている。すなわち,区間Bの方が得られた推定値の信頼度が高く,モデル推定に適した区間であることが分かる。なお,詳細は記述しないが,区間Bで得られた推定値を用いたモデルは,3.2節で挙げたモデル更新の3条件の残り2つ(条件B, C)も満たしている。
次に,区間Bで得られた推定値をモデルのパラメータとして設定し,表2と同じ設定でシミュレーションを行った結果を図9に示す。
なお,このシミュレーションでは,モデルの更新による制御性能の改善を確認しやすくするため,推定時(図6)に2:30~5:00の区間で追加した分散1.0の大きな外乱は与えていない。
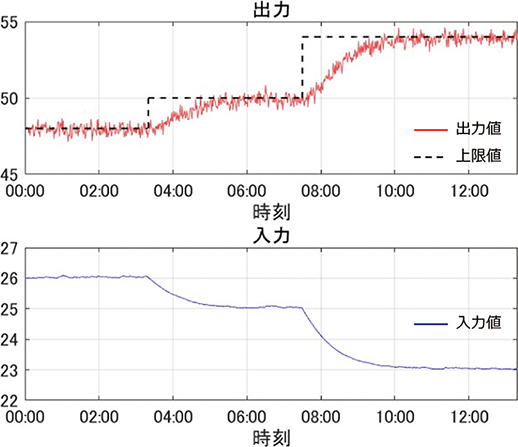
図9 推定パラメータを用いたシミュレーション
このシミュレーションではモデルのゲインがプラントの実際の値に近づいたことで,オーバーシュートによる上限値違反を起こすことなく目標値へと追従していることが確認できる。
以上のように,提案手法は制御・最適化された通常操業中のプラントデータからモデル推定に適した区間を選択し,モデルを推定することができる。これにより,必要な精度を満たしたパラメータ値でモデルを更新できる。また,それにより,制御性能を維持できることを示した。
6.おわりに
本報告では通常操業中のプラントデータからプラントのモデルを推定し,自動更新する技術について説明した。本技術はCO2削減など高度制御による顧客価値の維持に有効だと考えられる。なお,この技術を用いたプラントモデル更新機能がSORTiAの新機能として開発済みであり,SORTiA-IMB (IMBはIntelligent Model Builderの略)として提供される。
通常操業中のプラントデータはモデル推定に適さない区間を多く含む。そのため,プラントの時系列データを複数区間に分割し,その中から推定に利用可能な区間を自動で選択する手法を新たに開発した。これは,モデルのパラメータの確率分布を推定し,分布の分散が小さい区間を選択することで実現している。本手法は通常操業中のデータがあれば適用可能なので,ユーザーの負担が小さい,プラント操業への影響が無いという利点がある。
本手法実現には,動的モデルのパラメータの確率分布を推定する手法が必要となった。これは,遂次モンテカルロ法の一種であるパーティクルフィルタに基づく手法により,パラメータをベイズ推定することで実現した。
また,モデル予測制御で制御・最適化されたプラントを想定した数値シミュレーションを行い,提案手法によりモデル更新に適した区間が選択されること,その区間で推定されたモデルを用いることで更新前より制御性能が改善されることを示した。
アズビルは,今後も制御・最適化技術を通じて,CO2削減やオペレーション負荷低減に貢献していきたいと考えている。
<参考文献>
(1) 田原鉄也,藤江真也.“モデル予測制御に基づいた高度プロセス制御ソリューション”,azbil Technical Review, 2014年,Vol. 55, pp. 40-48,アズビル株式会社
(2) S . Yamauchi, T. Watanabe, J. Nishiguchi. Recursive Process Model Update Based on Parameter Posterior Distribution, the 22nd IFAC World Congress, 2023
(3) N. Chopin, O. Papaspiliopoulos. An Introduction Sequential Monte Carlo, Springer, 2020
(4) 樋口知之,予測にいかす統計モデリングの基本:ベイズ統計入門から応用まで,2011年,講談社
(5) 足立修一,丸田一郎,カルマンフィルタの基礎,2012年,東京電機大学出版局
<商標>
SORTiAはアズビル株式会社の商標です。
<著者所属>
田原 鉄也 アズビル株式会社 AIソリューション推進部
川越 貴啓 アズビル株式会社 AIソリューション推進部
この記事は、技術報告書「azbil Technical Review」の2025年04月に掲載されたものです。
- 2025年発行号
- 巻頭言:シン・オートメーションの時代
- 特集に寄せて
- スマートフォンを用いた現場エンジニアリングの最適化
- ビルシステムにおけるネットワーク構成と物理配置を統合した自動可視化技術の開発
- 熱画像カメラでの移動体鮮明化技術の開発
- 機械学習による製品品質影響因子の特定
- パラメーター確率分布を用いたプラントモデル自動更新技術
- マルチセンサに最適化したインターリーブ型ΔΣA/D変換回路の開発
- 大規模言語モデルを基盤とした法務契約文書リスク評価手法
- 個別エリア対応ユーザターミナル:ネオパネル2(QJ-1301)
- デジタル指示調節計 形 C2A/C2B/C3A/C3B 機能拡充と汎用性向上
- サファイア隔膜真空計(形V8)の開発
- 電力スマートメーター対応水道用無線端末(型式:ENCUW-H8A0)の開発
- 2024年発行号
- 2023年発行号
- 2022年発行号
- 2021年発行号
- 2020年発行号
- 2019年発行号
- 2018年発行号
- 2017年発行号
- 2016年発行号
- 2015年発行号
- 2014年発行号
- 2013年発行号
- 2012年発行号
- 2011年発行号
- 2009年発行号
- 2008年発行号
- 2007年発行号
- 2006年発行号
