マルチセンサに最適化したインターリーブ型\(\Delta\)\(\Sigma\)A/D変換回路の開発
キーワード:カスタムIC,\(\Delta\)\(\Sigma\)A/D変換回路,マルチセンサ,デジタルフィルタ
産業用計測機器において,複数センサを使ったマルチセンサシステムによる高精度化は広く利用されている。例えば圧力や温度などの複数センサを搭載して,主となるセンサの補正や環境変化へのデータ補正などを行っている。補正演算をする場合,複数センサ間のレイテンシを小さくし,高精度かつ低消費電力でA/D変換(アナログ・デジタル変換)することが必要となる。この課題を解決するため,複数センサに最適化したA/D変換回路の方式として,インターリーブ型ΔΣA/D変換回路を提案し,回路の試作と評価による機能検証を行った。
1.はじめに
産業用計測機器において,高精度の測定結果を得るために複数センサを補正等に利用するマルチセンサシステムは広く利用されている。例えば,圧力計測において,メインで使用する圧力センサの特性を補正するために,サブの圧力センサや温度センサも利用される。
高精度計測のために\(\Delta\)\(\Sigma\)型A/D変換方式(1), (2), (3)が一般的に用いられるが,市販の\(\Delta\)\(\Sigma\)A/D変換器では複数のセンサのA/D変換時に入力チャンネル間のレイテンシ(入力サンプリングからA/D変換結果までの時間差)が大きいため,センサ間の相関がとれなくなり補正等に用いる際の誤差が大きくなってしまう。一方,レイテンシを下げるために複数のA/D変換回路を同時に用いる場合は,消費電力が過大になってしまう。例えば,2線式のフィールド機器等のように4-20mAの電流で動作する計測機器においては,消費電流4mA以下で動作する必要があるため,A/D変換機能の消費電力を低減することは,複数の機能を製品に実装するうえで必須となる。
このようにマルチセンサのセンシング,すなわちA/D変換回路においては,複数センサ間の相関やレイテンシの低減と,消費電力の低減が重要な課題である。これらの課題を解決するため,マルチセンサシステムに最適化したA/D変換回路を新規設計し,弊社独自のカスタムICとして実装,機能評価を行った。その結果を報告する。
2.\(\Delta\)\(\Sigma\)ADCのマルチセンサシステムへの適用
2.1 \(\Delta\)\(\Sigma\)ADCの基本構成(1), (2), (3)
\(\Delta\)\(\Sigma\)型A/D変換回路(以下\(\Delta\)\(\Sigma\)ADCと表記)は,高精度のA/D変換回路として,アナログインターフェース回路に一般的に使用されている。\(\Delta\)\(\Sigma\)ADCは,図1で示されるように,アナログ回路で構成される積分器,量子化器(コンパレータ),そして入力信号との差分がフィードバックされる\(\Delta\)\(\Sigma\)変調回路と,後段のデジタルフィルタで構成され,前段の\(\Delta\)\(\Sigma\)変調回路では入力されたアナログ電圧をデジタル変調信号に変換し,後段のデジタルフィルタでは,そのデジタル変調信号の時間平均とデシメーション(ダウンサンプリング)を行う。
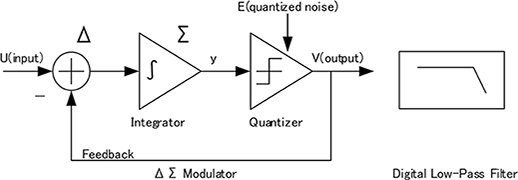
図1 \(\Delta\)\(\Sigma\)ADCの概略図
\(\Delta\)\(\Sigma\)ADCは,オーバーサンプリングとノイズシェーピングにより,高精度のA/D変換を実現している。原理を図2に示す。
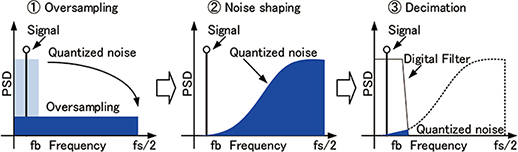
図2 \(\Delta\)\(\Sigma\)ADCの高S/N実現の原理
オーバーサンプリングとは,入力信号を信号帯域より高速にサンプリングする方式である。熱雑音や量子化雑音などの雑音成分は,ナイキスト周波数(サンプリング周波数の1/2)の範囲で分布するため,高速でサンプリングすることで雑音成分を広い周波数帯域に分布させて,信号帯域内の雑音を低減することができる。
ノイズシェーピングとは,量子化回路で発生する量子化雑音を高周波数領域に分布させることである。\(\Delta\)\(\Sigma\)変調回路にて,入力信号と出力の変調信号との差分を積分するフィードバックループを構成することで,低周波数領域の雑音成分が抑圧される。高周波数領域にノイズシェーピングされた量子化雑音は,ローパス特性のデジタルフィルタでの平均化処理で除去できる。
ノイズシェーピングの効果は,\(\Delta\)\(\Sigma\)変調回路で信号を積分する回数(次数)が大きいほど効果が大きくなり,量子化雑音は高次のハイパス特性を持つことになる。量子化雑音を除去するためには,後段のデジタルフィルタが量子化雑音以上の次数のローパス特性を持つ必要がある。例えば,\(\Delta\)\(\Sigma\)変調回路の次数が2次の場合,デジタルフィルタは,3次のローパス特性が必要となる。
2.2 デジタルフィルタのレイテンシ
\(\Delta\)\(\Sigma\)ADCでよく使用されるデジタルフィルタとして,SINCフィルタと呼ばれる回路が挙げられる。ここでは,SINCフィルタの例として,2次変調の\(\Delta\)\(\Sigma\)ADCに使用されるSINC3フィルタについて,図3にて示す。

図3 SINC3フィルタの概略図
SINC3フィルタは3つの加算器,ダウンサンプリング(図3でのスイッチ),3つの減算器で構成され,ローパスフィルタを多段に接続するよりも,少ない回路構成で高次のフィルタ回路を構成できる利点がある。(4)
ここで入力信号周波数に対するサンプリング周波数の比(オーバーサンプリング比)をNとしたとき,SINC3フィルタではN個のサンプリングごとにA/D変換結果が出力される。ただし,起動時などのA/D変換動作開始時や入力信号を切り替えた時など,フィルタ内部のレジスタ回路をリセットした後に再び出力を得るまでには,デジタルフィルタでの平均化処理のために\(\Delta\)\(\Sigma\)変調回路の3N点のデータが必要となる。つまりリセット直後にデータを得るためには,データ更新周期の3倍の時間が必要となる。図4に,リセット直後に必要な待ち時間(レイテンシ)を示す。

図4 \(\Delta\)\(\Sigma\)ADCのデジタルフィルタリセット直後のデータ更新のタイミング
2.3 \(\Delta\)\(\Sigma\)ADCのマルチセンサシステムへの適用
\(\Delta\)\(\Sigma\)ADCをマルチセンサシステムに適用する場合を図5に示す。市販の\(\Delta\)\(\Sigma\)ADCを用いる場合は,図5の左のようにマルチプレクサを用いてセンサの入力を切り替えるか,図5の右のようにセンサの数に合わせて\(\Delta\)\(\Sigma\)ADCを複数搭載する方法が考えられる。
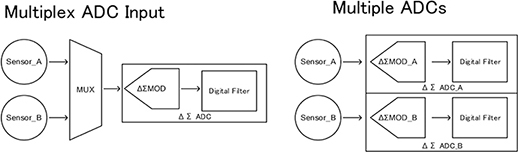
図5 マルチセンサシステムへの\(\Delta\)\(\Sigma\)ADC適用の概略図
センサの入力を切り替える場合は,切り替えのタイミングでデジタルフィルタのリセットが必要になるため,2.2で示したように,入力を切り替えるたびにデータ更新周期の3倍のレイテンシが発生することになる。例えば,図6に示したように2系統のセンサ信号を1点ずつA/D変換する場合,データが出力する度にΔΣ変調回路の3N点分のレイテンシが発生するため,各センサのデータ更新周期は変調信号6N点となり,切り替えを行わない場合の6倍長くなることになる。
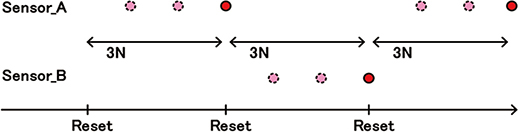
図6 複数のセンサのA/D変換を行った場合のデータ更新のタイミング
センサの数に合わせて\(\Delta\)\(\Sigma\)ADCを複数搭載する場合は,切り替えが必要ないため,図6で示したようなレイテンシは発生しない。しかし,この方式は\(\Delta\)\(\Sigma\)ADCが複数必要になる分,消費電力の増加につながるため,消費電力が制限されている場合には,製品への実装が難しくなる。
3.インターリーブ型\(\Delta\)\(\Sigma\)ADC(6)
3.1 回路の概要
2.3で示した課題を解決するため,デジタルフィルタのリセットを必要とせず,かつ\(\Delta\)\(\Sigma\)変調回路1個に相当する回路規模で複数チャネルのA/D変換を行える回路方式を提案する。
まず図7に従来型の\(\Delta\)\(\Sigma\)変調回路の回路図を示す。
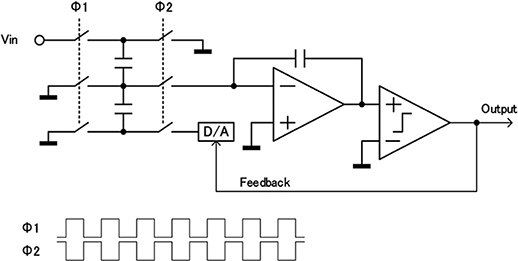
図7 従来型の\(\Delta\)\(\Sigma\)変調回路の回路図(上)とタイミングダイアグラム(下)
図7に示した回路は,スイッチトキャパシタと呼ばれる回路方式であり,アナログ電圧を容量への充電電荷として入力し,タイミングダイアグラムに示したタイミングでスイッチの状態をOpenとCloseとで切り替えて,電荷の充放電することで入力信号の積分を行う。従来型の回路では,オペアンプの反転入力端子と出力端子に接続した積分容量に,入力信号の積分値が電荷として保存される。
図8に提案する\(\Delta\)\(\Sigma\)変調回路の回路図を示す。
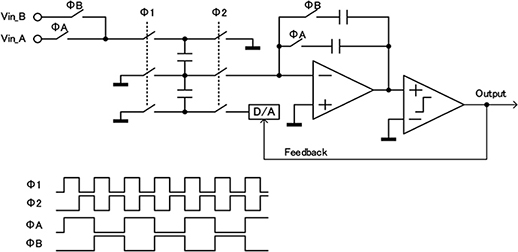
図8 新規設計のインターリーブ型\(\Delta\)\(\Sigma\)変調回路の回路図(上)とタイミングダイアグラム(下)
新規設計の回路は,インターリーブ型\(\Delta\)\(\Sigma\)変調回路と呼称している。特徴は,複数の入力チャネルの信号を切り替える選択回路と,入力チャネル数と同数の積分容量を持つことである。例えば,チャネルAの積分を行うときには,チャネルAのスイッチをClose,チャネルBをOpenにすることで,チャネルAの入力信号が積分される。その間はチャネルBの充電電荷,すなわち信号の積分値が保存される。図8のタイミングダイアグラムに示したように,入力チャネルA,Bの選択を,積分動作1回ごとに切り替えることで,複数の入力チャネルの積分動作を並列に行うことができる。
提案するインターリーブ型ΔΣ変調回路を持つA/D変換回路をインターリーブ型\(\Delta\)\(\Sigma\)ADCと呼称し,2入力の回路例での構成を図9に示す。
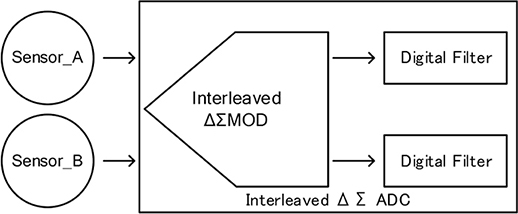
図9 インターリーブ型\(\Delta\)\(\Sigma\)ADCの全体構成
インターリーブ型\(\Delta\)\(\Sigma\)変調回路から入力チャネル2系統に対応する変調信号が並列に出力されるため,後段には2系統のデジタルフィルタを実装する。図9では簡易のためにデジタルフィルタを2系統並列に示しているが,内部の共通化により単純な並列実装ではない(4)。
2系統のデジタルフィルタで,量子化ノイズの除去とデシメーション(ダウンサンプリング)を行うことで,リセットを行わずに複数チャネルをA/D変換することができる。このインターリーブ型\(\Delta\)\(\Sigma\)ADCのデータ更新タイミングを,図10に示す。
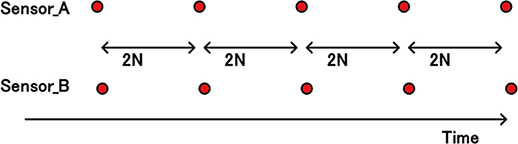
図10 インターリーブ型\(\Delta\)\(\Sigma\)ADCのデータ更新のタイミング
入力チャネル2系統の積分動作を交互に行うため,各チャネルの変調信号N点を出力するには2N点分の時間がかかるが,デジタルフィルタのリセットが不要なので,図6で示したレイテンシが原理的に発生しなくなる。チャネル間の時間差は,オーバーサンプリングを行う\(\Delta\)\(\Sigma\)変調回路のサンプリング周期程度であるため,入力信号の時間変化に対して十分に短い時間となる。
3.2 試作回路の設計
3.1で示したインターリーブ型\(\Delta\)\(\Sigma\)変調回路を実際に検証するため,IC用の試作回路を設計し,評価によって動作確認を行った。図11に,試作を行ったインターリーブ型\(\Delta\)\(\Sigma\)変調回路の回路図を示す。
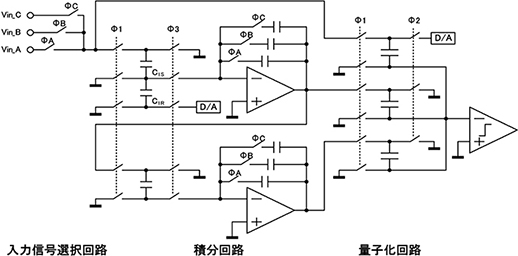
図11 試作版インターリーブ型\(\Delta\)\(\Sigma\)変調回路の回路図
(一部を簡略化して記述している)
図11の回路は,2次\(\Delta\)\(\Sigma\)変調回路(5)として設計しており,入力信号と出力の変調信号との差分の積分を2段階行う。後段の量子化回路で,入力信号と1段目,2段目の積分回路の出力を加算した信号をA/D変換して,変換結果を積分回路のD/A変換回路にフィードバックする。
また,図11では簡略化のためにシングルエンド入力の回路として記述しているが,実際の試作回路は,入力信号のコモンモードノイズを抑制するために,差動入力型として設計している。
\(\Delta\)\(\Sigma\)変調回路のサンプリング周波数は100kHzとした。電源電圧は3.3V,消費電流は230uA程度である。試作回路は,3チャネルを並列でA/D変換する設計としており,入力信号の選択回路と積分容量は3チャネル分搭載している。今回は,3系統の入力チャネルA,B,Cに対して,チャネルAを高精度が求められるメインセンサ用,チャネルB,Cをサブセンサ用と定めて,チャネルAの平均処理回数を高めるために,並列変換時のチャネルの切り替え順を,チャネルA→B→A→Cの順とした。これにより,チャネルAのサンプリング周波数が,チャネルB,Cの2倍となり,2.1で示したオーバーサンプリングによる雑音の低減の効果が大きくなる。1回の入力信号のサンプリングと積分動作の時間が10us(100kHz)となるようタイミング制御を行うため,各チャネルのサンプリング周期は,チャネルAが20us(50kHz),チャネルB,Cが40us(25kHz)となる。
3.3 試作回路の実装と評価
インターリーブ型\(\Delta\)\(\Sigma\)ADCの機能実証のため,図11で示した回路を搭載したICを試作し,A/D変換の機能評価を行った。IC内部の試作回路を図12に示す。試作回路は,180nm世代のCMOSプロセスで設計した。
図12 試作ICのマスクパターン図(インターリーブ型\(\Delta\)\(\Sigma\)ADC周辺)
次に,この試作回路の評価について以下に示す。
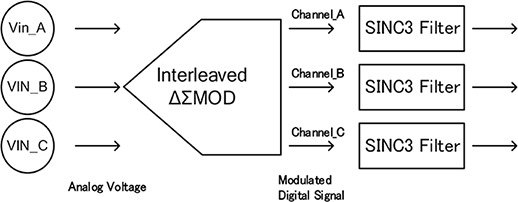
図13 インターリーブ型\(\Delta\)\(\Sigma\)ADCの評価
インターリーブ型\(\Delta\)\(\Sigma\)ADCの3チャネルの入力端子にそれぞれDC電圧を入力し,出力された変調信号に対してSINC3フィルタを用いて雑音除去とダウンサンプリングを行い,A/D変換値を取得した。概略は図13に示す。
評価においては,各チャネルに与えた入力電圧とA/D変換値が対応しているかを確認し,複数チャネル並列のA/D変換機能を検証した。A/D変換値の平均値と標準偏差を求め,その平均値と入力電圧との関係からゲイン(感度)を導出し,標準偏差をA/D変換回路の雑音とした。
同じ入力信号帯域での比較を行うため,各チャネルのSINC3フィルタの平均長Nは,それぞれのデータ更新周期を10msになるよう,チャネルAは500,チャネルB,Cは250とした。
図14に,各チャネルのA/D変換値を示し,図15に,チャネルAのA/D変換値の偏差を拡大した図を示す。また,表1に解析結果を示す。
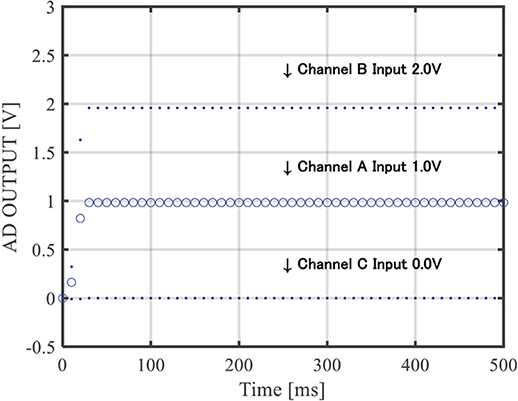
図14 DC電圧入力時のA/D変換値
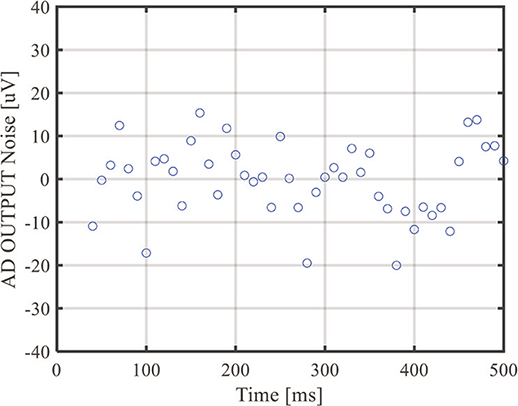
図15 チャネルAのA/D変換値の偏差
表1 DC電圧入力時のA/D変換値の平均値と標準偏差
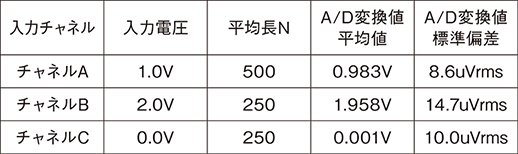
図14,図15および表1に示した評価結果からの考察を以下に示す。
各チャネルの入力電圧と表1のA/D変換値の平均値を比較すると,1.7%程度の誤差があるが,傾向としては入力電圧と一致している。インターリーブ型\(\Delta\)\(\Sigma\)変調器を用いた複数チャネル並列のA/D変換動作は想定通りに動作していると考えられる。1.7%の誤差については,入力電圧の絶対値が大きい条件で誤差が大きいことから,入力電圧に対するゲイン(感度)誤差が発生していると考えられる。この誤差は,図11のスイッチトキャパシタ回路において,入力信号用の容量と出力の負帰還用の容量とがミスマッチを起こしたことが原因であると考えられる。IC回路内の寄生素子抽出を行った結果,寄生容量が原因で前述の箇所の容量ミスマッチが起こっていたことが分かった。ゲイン誤差はキャリブレーション等で補正できるので大きな問題ではないと考えている。
次に,表1のA/D変換値の標準偏差をA/D変換時の雑音として解析を行う。A/D変換値の標準偏差は8.67~14.7uVrms程度であり,雑音のピーク幅は標準偏差の6倍として,52~88uV程度となる。
雑音とフルスケール電圧との比からノイズフリーで使用できる実効的な分解能を導出する。試作回路は,差動入力型かつ基準電圧3.3Vであるため,入力電圧の範囲は-3.3Vから+3.3V,フルスケール電圧は6.6Vとなる。雑音のピーク幅とフルスケール電圧の比は216~217程度であるため,実効的な分解能は16~17bit程度となる。
また,チャネル間で雑音を比較すると,チャネルAの値がチャネルB,Cと比較して小さい。3. 2に記載した通り,チャネルAはメインセンサでの使用を想定して,他のチャネルよりオーバーサンプリング比を上げる設計にしていたため,雑音をより低減できたと考える。
最後に,今回の試作で課題とした,A/D変換時のセンサ間のレイテンシの低減と,消費電力の低減について考察する。
レイテンシについては,複数チャネル並列でのA/D変換動作を達成できたことから,入力チャネルの切り替え時に生じるレイテンシは低減できた。複数チャネル間のA/D変換の時間差は,\(\Delta\)\(\Sigma\)変調回路のサンプリング周期である10~20us程度であり,10ms程度のデータ更新周期に対して十分に小さい値である。複数チャネルごとのA/D変換器を用いないため,その消費電力も市販品を使う場合に比べて削減できる。
4.おわりに
本報告により,複数チャネルを並列でA/D変換可能なインターリーブ型\(\Delta\)\(\Sigma\)ADCの試作と評価を行い,実際に複数チャネル並列でのA/D変換動作を確認できた。精度に関しても,データ更新周期10msで16bit以上の精度を実現できることから,産業用計測機器の用途としても幅広く利用できると考える。
今回の報告を通じて,ディスクリートの部品では解決が難しい設計課題に対して,カスタムICが有用であると示せたと考える。さらに回路の消費電力を最適化することや,寄生容量由来のゲイン誤差の対策等の性能改善など,更なる性能向上を今後のテーマとして取り組み,今後も弊社製品の性能強化改善に向けたIC設計技術を継続的に強化・発展させていきたいと考えている。
<参考文献>
(1) J. C. Candy and G. C. Temes, Oversampling Delta-Sigma Data Converters. IEEE Press, 1992.
(2) S. R. Norsworthy, R. Schreier, and G. C. Temes, Delta-Sigma Data Converters. IEEE Press, 1997.
(3) Schreier and G. C. Temes, Understanding Delta-Sigma Data Converter. Wiley-Interscience, 2005.
(4) Hideki Kuribayashi and Tetsuya Kajita, “Area-Efficient Decimation Filter with 50/60Hz Power-Line Noise Suppression for ΔΣA/D Converters”, SICE Journal of Control, Measurement, and System Integration, Vol. 10, No. 3, pp. 165-169, May 2017.
(5) J.Silva, U.Moon, J.Steensgaard and G.C.Times, “Wideband low distortion delta sigma ADC topology”, E lectronics L etters, vol.37, no.12, pp.737-738, June 7 2001.
(6) Hiroaki Teshima, Taichiro Kato, and Tetsuya Kajita, “No-Latency Interleaved Delta-Sigma ADC for Multiple-Sensor Interfacing Circuits”, Proceedings of SICE Festival 2024 with Annual Conference, pp.833-837.
<著者所属>
手島 紘明 アズビル株式会社 技術開発本部基幹技術部3グループ
加藤 太一郎 アズビル株式会社 技術開発本部基幹技術部3グループ
梶田 徹矢 アズビル株式会社 技術開発本部
この記事は、技術報告書「azbil Technical Review」の2025年04月に掲載されたものです。
- 2025年発行号
- 巻頭言:シン・オートメーションの時代
- 特集に寄せて
- スマートフォンを用いた現場エンジニアリングの最適化
- ビルシステムにおけるネットワーク構成と物理配置を統合した自動可視化技術の開発
- 熱画像カメラでの移動体鮮明化技術の開発
- 機械学習による製品品質影響因子の特定
- パラメーター確率分布を用いたプラントモデル自動更新技術
- マルチセンサに最適化したインターリーブ型ΔΣA/D変換回路の開発
- 大規模言語モデルを基盤とした法務契約文書リスク評価手法
- 個別エリア対応ユーザターミナル:ネオパネル2(QJ-1301)
- デジタル指示調節計 形 C2A/C2B/C3A/C3B 機能拡充と汎用性向上
- サファイア隔膜真空計(形V8)の開発
- 電力スマートメーター対応水道用無線端末(型式:ENCUW-H8A0)の開発
- 2024年発行号
- 2023年発行号
- 2022年発行号
- 2021年発行号
- 2020年発行号
- 2019年発行号
- 2018年発行号
- 2017年発行号
- 2016年発行号
- 2015年発行号
- 2014年発行号
- 2013年発行号
- 2012年発行号
- 2011年発行号
- 2009年発行号
- 2008年発行号
- 2007年発行号
- 2006年発行号
